◻ Stab2D-NL - Rechenalgorithmen

(Genauere Erläuterungen finden Sie bei den Informationen zu meiner Dissertation.)

Allgemeines

Eine sehr leistungsfähige Methode zur nichtlinearen Berechnung von Stahlbetonkonstruktionen ist das Übertragungsverfahren [2,3]. Mit einer zuvor berechneten Momenten-Verkrümmungs-Beziehung ist es möglich, die jeweils richtigen Verkrümmungen und Biegesteifigkeiten bei der Stabberechnung zu benutzen. Damit lässt sich nicht nur der Übergang ungerissen / gerissen gut abbilden, auch die Berechnung mit Fließen der Bewehrung ist ohne Einfügen plastischer Gelenke sowie ohne Lastinkremente in nur einem Lastschritt möglich.
Ein Nachteil dieser Methode ist jedoch, dass einerseits die Mk-Linie im Voraus bestimmt werden muss und andererseits nur Durchlaufträger oder Stützen mit vertretbarem Aufwand berechnet werden können. Durch die Kopplung von nichtlinearer Querschnittsberechnung, Übertragungsverfahren und FE-Methode ergibt sich jedoch die Möglichkeit, auch größere ebene Rahmenstrukturen nichtlinear berechnen zu können. Eine Erweiterung auf den 3D-Fall ist ebenso möglich.
Dazu wird jeder Balken des Tragwerkes im Volleinspannzustand mit dem Übertragungsverfahren berechnet. Die benötigten Werte für Verkrümmung und Biegesteifigkeit sowie Dehnung e0 und Dehnsteifigkeit werden jeweils für die aktuelle Beanspruchung Nx / My mittels einer nichtlinearen Querschnittsberechnung bestimmt. Unter Nutzung der 1-Zustände des Übertragungsverfahrens ist es dann möglich, die lokale Steifigkeitsmatrix für den Balken sowie den zugehörigen Kräftevektor zu ermitteln. Die Lösung der globalen K-Matrix liefert im Anschluss die Knotenverformungen.

Berechnung der Steifigkeiten

An jedem Stababschnitt wird zu den aktuellen Schnittgrößen Nx / My der Dehnungszustand und damit auch die zugehörigen Steifigkeiten bestimmt. Für eine realitätsnahe Berechnung ist neben der korrekten Modellierung der Spannungs-Dehnungs-Beziehungen die Annahme über die versteifende Mitwirkung der gerissenen Betonzugzone wichtig. Der benutzte Ansatz geht auf Quast (1977/80/81) und Espion (1985) [4] zurück und liefert für baupraktische Belange eine ausreichend gute Übereinstimmung mit Versuchsergebnissen. Weitere Ausführungen zur Modellierung der Zugzone sind im Heft 415 des DAfStb [5] zu finden.
Im vorliegenden Programm Stab2D-NL dienen die Routinen zur Querschnittsberechnung des Programms INCA2 [6] der Steifigkeitsermittlung, so dass alle auch in INCA2 berücksichtigten Effekte (z.B. Schwinden, Kriechen, Vorspannung oder nachträglich ergänzte Querschnitte) implementiert wurden.

Übertragungsverfahren

Die Berechnung beginnt mit der vorläufigen Unterteilung des Stabes in Elemente der Länge dx. Sind die Zustandsgrößen auf der linken Seite eines Elements sowie die äußeren Belastungen bekannt, so können mittels der Übertragungsgleichungen die Zustandsgrößen auf der rechten Seite ermittelt werden. In Gleichung (2) ist beispielhaft die Berechnung des Biegemoments unter Berücksichtung von Theorie 2. Ordnung dargestellt, in Gleichung (1) die Berechnung der vertikalen Verformung Dw_ver. Der Näherungsansatz für die Berücksichtigung der Normalkraft ist für kleine Elemente der Länge dx ausreichend genau.



Zur Berücksichtigung des nichtlinearen Verhaltens des Stahlbetons wird an jedem Stababschnitt jeweils zur aktuellen Schnittgrößenkombination der Dehnungszustand sowie die zugehörigen tangentialen Steifigkeiten berechnet. Ändert sich jedoch die Biegesteifigkeit von einem Segment zum nächsten sehr stark, so wird dieser Abschnitt feiner geteilt, um die sich verändernde Steifigkeit genauer zu erfassen.



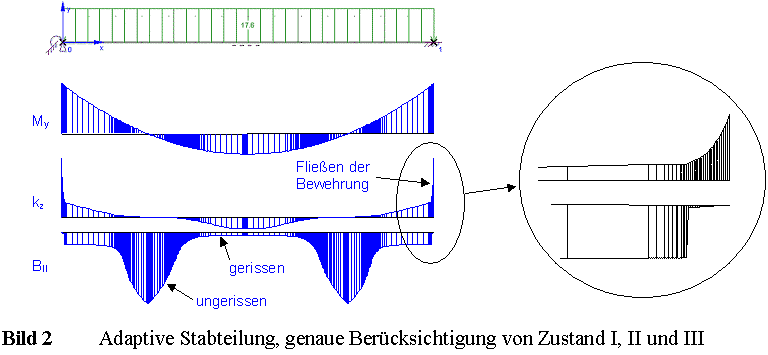
Durch diese adaptive Teilung wird erreicht, dass die Diskretisierung des Tragwerkes genau so fein wie erforderlich durchgeführt wird (Bild 2): Bereiche mit geringen Steifigkeitsänderungen werden in große Abschnitte geteilt, Bereiche mit steilen Gradienten entsprechend in kleine Abschnitte.
Mit dieser gezeigten Formulierung ist es möglich, bei gegebenen Startwerten am linken Ende des Balkens die Zustandsgrößen für den gesamten Balken zu berechnen. Die zunächst unbekannten Startwerte werden auf iterativem Wege ermittelt (entspricht dem Lösen einer DGL als Randwertaufgabe).

FE-Methode

Wurden bereits beim Übertragungsverfahren Inkremente (DNx / DQz / DMy) benutzt, um die Auswirkungen der Startwerte (Nx / Qz / My) auf die Endwerte (wx, wy, j) zu untersuchen, so können diese 1-Zustände ebenfalls zur Bestimmung der Lokalen Steifigkeitsmatrix benutzt werden. Dazu wird anschaulich an jedem Freiheitsgrad eine 1-Verformung aufgebracht und die nötigen Kräfte bestimmt, um das System in dieser ausgelenkten Lage im Gleichgewicht zu halten. Der sich ergebende Kräftevektor repräsentiert damit ine Spalte der K-Matrix.
Nach Berechnung aller Stäbe mittels Übertragungsverfahren kann damit die globale Steifigkeitsmatrix erstellt und das lineare Gleichungssystem gelöst werden. Die sich ergebenden Knotenverformungen stellen den Ausgangspunkt für den nächsten Iterations- oder Lastschritt dar.

Iteration und Konvergenz

Insbesondere das Übertragungsverfahren hat sich bei den bisherigen Berechnungen auch nahe des Grenzzustandes der Tragfähigkeit als sehr stabil erwiesen. Durch die anschließende integrale Betrachtung eines längeren Stabes in der lokalen Steifigkeitsmatrix, wird auch die FE-Iteration günstig beeinflusst.
Nichtsdestotrotz gibt es auch nach ständiger Weiterentwicklung der Iterationsalgorithmen in einigen Fällen Konvergenzprobleme im Grenzzustand der Tragfähigkeit, wenn die Biegesteifigkeit zum Beispiel auf ca. 1/1000 des ungerissenen Wertes abgefallen ist. Diese Probleme werden jedoch durch die berücksichtigten Effekte wie Dehnung der Systemachse bei Momentenbeanspruchung oder Theorie 3. Ordnung hervorgerufen, sind damit grundlegender Natur und äußern sich in einer Verkleinerung des Konvergenzradius. Eine nachhaltige Verbesserung der Konvergenz ergibt sich damit durch das Berechnen eines guten Startwertes für den nächsten Iterationsschritt sowie genauer Kenntnis des Iterationsgebietes.

Literatur (Auswahl)

1. G. Griebenow, Richtlinie für das Aufstellen und Prüfen EDV-unterstützter Standsicherheitsnachweise. Der Prüfingenieur, H. 19, Oktober 2001, S. 50-56.
2. U. Quast: Anwendung des Reduktionsverfahrens zur Bemessung von Stahlbeton-Stabwerken nach Theorie II. Ordnung. Beton- und Stahlbetonbau 5, 1976, S. 115-118
3. U. Quast: Zum nichtlinearen Berechnen im Stahlbeton- und Spannbetonbau. Beton- und Stahlbeton 89 (1994), H. 9, S. 250-253, H. 10, S. 280-284.
4. B. Espion: Contribution à l`analyse non linéaire des ossatures planes. Thése de Doctorat, Université Libre de Bruxelles 1985.
5. U. Quast u. D. Busjaeger: Programmgesteuerte Berechnung beliebiger Massivbauquerschnitte unter zweiachsiger Biegung mit Längskraft (Programm MASQUE), DAfStb, Heft 415, 1990