◻ Beispiel 1 - Zweifeldträger,
    Vergleich lineare und nichtlineare Berechnung

Eingangswerte

Spannweite	Leff = 7,00 m	Um die Rechnung zu vereinfachen wird sowohl für die positiven als auch für die negativen Biegemomente ein einziger Querschnitt benutzt. Die Bewehrung wurde entsprechend gewählt.
Auflagerbreite	b = 0,60 m (zur Momentenausrundung)
Belastung	f = 10,5 kN/m
Querschnitt	b / h = 0,30 / 0,30 m
Biegesteifigkeit	EI = 21600 kNm²
Baustoffe	Beton C30/37 nach DIN 1045-1 (neu) Betonstahl BSt 500 As,oben = 5,17 cm² As,unten = 2,64 cm²

Statisches System mit Belastung

Für das mittlere Auflager wurde eine Auflagerbreite mit b = 0,60 m definiert. Dadurch wird während
der Rechnung eine automatische Ausrundung des Biegemomentenverlaufs erreicht.

Lineare und nichtlineare Berechnung des Zweifeldträgers

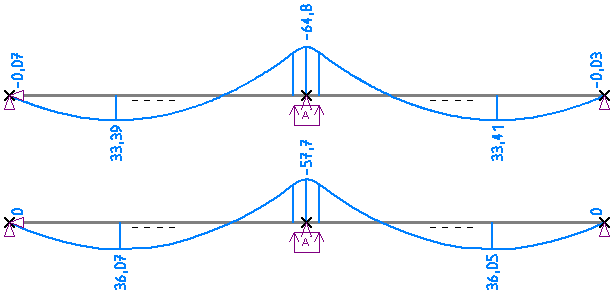
	In nebenstehendem Bild ist der Momentenverlauf dargestellt (oben nichtlinear, unten linear). Deutlich zu erkennen ist jeweils die Momentenausrundung über dem mittleren Auflager. Die kleinen Momente an den gelenkigen Auflagern ergeben sich durch die gewählte Abbruchgenauigkeit von 0,1 für die Iteration.
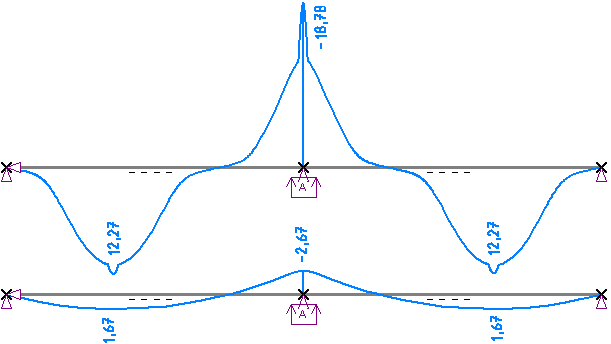
	Am Verkrümmungsverlauf erkennt amn deutlich die Unterschiede zwischen der linearen und nichtlinearen Rechnung. Die Bewehrungsmenge wurde gerade so gewählt, dass die Bewehrung sowohl im Feld als auch über dem mittleren Auflager plastiziert, was deutlich an der stark erhöhten Verkrümmung zu erkennen ist. Infolgedessen gestaltet sich die Iteration im letzten Lastschritt sehr schwierig, da kleine Änderungen in den Schnittgrößen (Biegemoment + Normalkraft) zu sehr großen Änderungen in den Verformungskennwerten führen.
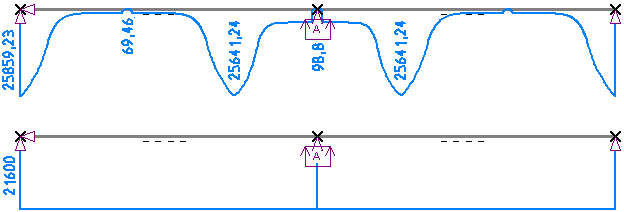
	Am Verlauf der tangentialen Biegesteifigkeit sind die gerissenen und ungerissenen Bereiche des Balkens sehr gut zu erkennen. In den Bereichen mit fließender Bewehrung fällt die Steifigkeit auf 1/300 bis 1/400 des linear-elastischen Wertes ab. Die im Vergleich zu EI = 21600 kNm² erhöhte Steifigkeit von B = 25859 kNm² in den ungerissenen Bereichen ist darauf zurückzuführen, dass in diesem Fall einerseits die Bewehrung berücksichtigt wurde, andererseits der Anfangs- Tangentenmodul des Betons höher ist als der ansonsten benutzte Wert von E = 32000 N/mm².
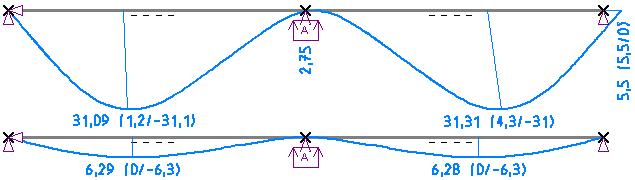
	Der Unterschied in den resultierenden Verformungen ist wohl am augenfälligsten (Überhöhung in der Zeichnung 75fach). Statt 6,3 mm in der linearen Rechnung ergibt sich in der nichtlinearen Rechnung ein knapp 5facher Wert für die vertikale Verschiebung in Feldmitte mit w = 31,1 mm. Anzumerken sei hier jedoch, dass der Balken mit der gezeigten Belastung sehr dicht am Grenzzustand der Tragfähigkeit ist. Bemerkenswert ist weiterhin die horizontale Verformung. Durch die Festhaltung des linken Auflagers summiert sich die horizontale Verschiebung zum rechten Auflager hin auf. Im linearen Fall verschiebt sich auf Grund Theorie 3. Ordnung das rechte Auflager um 0,03 mm nach links, der Abstand wird also kleiner. In der nichtlinearen Rechnung überwiegt dagegen der Anteil, der aus dem Aufreißen der Querschnitte resultiert, so dass sich in der Summe eine Verlängerung des Balkens um rund 5,5 mm ergibt.