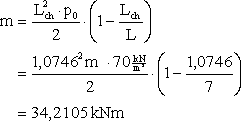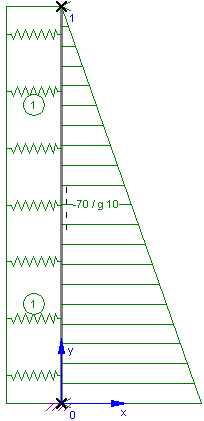
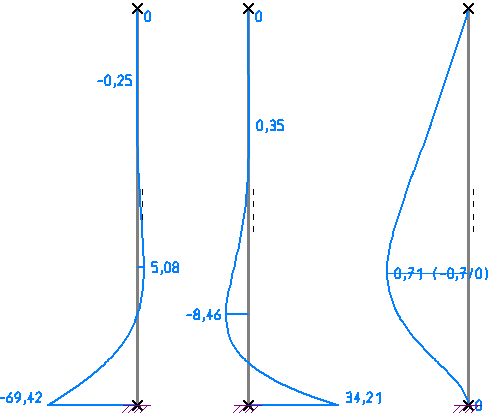
◻ Beispiel 3 - Kreiszylinderschale

Kreiszylinderschalen können als elastisch gebetteter Balken gerechnet werden. Dazu muss nur aus den Abmessungen der Schale eine äquivalente Bettungssteifigkeit C berechnet werden. Anschließend kann die Berechnung für einen 1 m breiten Streifen der Schale durchgeführt werden.

Eingangswerte Radius r = 10,00 m Dicke der Schale h = 0,20 m Länge der Schale L = 7,00 m E-Modul E = 32000 N/mm² Belastung   Gradient = 10 kN/m/m   Biegesteifigkeit EI = 21333,3 kNm² (1 m breiter Streifen) Schubsteifigkeit GA = 2666667 kN Bettungssteifigkeit C = (E * d) r² = 64000 kN/m²/m Charakteristische Länge Lchar = 0,7598 * (d * r)^0,5 = 1,0746 m

Statisches System mit Belastung

Ergebnisse

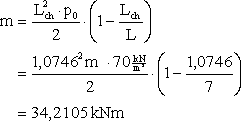
	In nebenstehendem Bild sind die Verläufe von Querkraft, Biegemoment und Verformung dargestellt. Man kann im oberen Bereich der Schale den ungestörten Membranspannungszustand erkennen. Im unteren Bereich der Fußeinspannung wird der Membranspannungszustand gestört, es treten Biegestörungen auf. Der Vergleich mit den Formeln entsprechend der Schalentheorie liefert:       In der Stab2D-NL-Rechnung ergab sich jedoch nur ein Biegemoment von m = 33,72 kNm. Der Unterschied ist darauf zurück zu führen, dass in Stab2D-NL auch die Querkraftverformung berücksichtigt wurde, in der obigen Formel (aus der Lösung der DGL) die Schubverformung jedoch vernachlässigt wurde (Schubsteifigkeit unendlich groß).	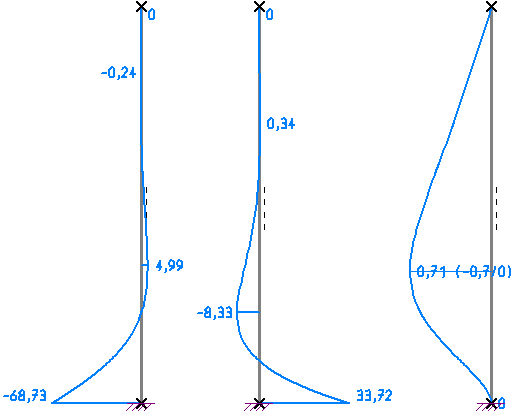Querkraft [kN] Biegemoment [kNm] Verformung [mm]
	Erst wenn man auch in Stab2D-NL die Schubsteifigkeit auf z.B. GA = 1E12 kN hoch setzt, erhält man den nebenstehenden Verlauf der Schnittgrößen Q und M sowie die Verformungen. Der berechnete Wert des Biegemoments stimmt gut mit der Stab2D-NL-Rechnung überein. Gleiches gilt für die hier nicht per Hand berechneten Werte der Querkraft oder der Verformungen. In der Summe bleibt jedoch zu erwähnen, dass man sich immer genau im Klaren sein sollte, was genau man mit einem Statik-Programm modelliert, was man vereinfacht, was vernachlässigt wird.