◻ Beispiel 4 - Fundamentstreifen nichtlinear

Eingangswerte

Spannweite	siehe Zeichnung
Belastung	Eigengewicht + Stützenlasten (bereits mit Teilsicherheitsbeiwerten)
Querschnitt	b / h = 1,20 / 0,40 m
E-Modul	E = 32000 N/mm²
Biegesteifigkeit	EI = 204800 kNm²
Schubsteifigkeit	GA = 6400000 kNm²
Dehnsteifigkeit	EA = 15360000 kN
Steifigkeit des Bodens	Es = 80.000 kN/m²/m
Bettungssteifigkeit	C = Es * b = 96.000 kN/m/m

Statisches System mit Belastung

Zur Vereinfachung wird im folgenden nur die Hälfte des symmetrischen Systems abgebildet. Die Randbedingung in der Mitte wird durch eine verschiebliche Einspannung erfasst. Die Einzellasten werden als Flächenlasten modelliert, wobei eine Stützenbreite selber von b_Stütze = 0,40 m sowie eine Ausbreitung der Last bis zur Mittellinie des Fundamentbalkens angenommen wird. Damit ergibt sich eine effektive Lasteinleitungsbreite von b_Last = 0,80 m.

Damit ergibt sich folgendes Modell:

Berechnung linear elastisch (Grenzzustand der Tragfähigkeit)

Mittels einer linear-ealstischen Rechnung ergibt sich nebenstehender Biegemomentenverlauf (oberes Bild). Nur die Lasten aus den Stützen verursachen die Momente, das Eigengewicht des Balkens sorgt nur für eine zusätzliche Verformung nach unten. Im unteren Bild sind die Bettungsspannungen als Reaktion des Bodens dargestellt. Der Einfachheit halber wird für die folgende nichtlineare Rechnung nur ein Querschnitt für den gesamten Balken modelliert. Die Bewehrung ist in etwa so angeordnet, dass der Balken jeweils etwas mehr als die max. positiven und negativen Biegemomente aufnehmen kann. Dazu wird in INCA2 ein Rechteckquerschnitt mit b / h = 1,20 / 0,40 m, Randabstand 0,05 m sowie obenliegender Bewehrung (As = 10 x d14 mm = 15,39 cm²) und untenliegender Bewehrung (As = 10 x d22 mm = 38,01 cm²) erzeugt. Man möge mir verzeihen, dass es d = 22 mm nicht unbedingt gibt.

Berechnung nichtlinear (nur Querschnittsebene)

Die Ergebnisse einer auf Querschnittsebene nichtlinearen Berechnung ergeben bereits deutlich andere Biegemomente. Nicht nur, dass sich die maßgebende Stelle des maximalen negativen Biegemoments verändert hat, auch die maximale Beanspruchung ist von M = -215,69 kNm auf M = -152,3 kNm gefallen. Ähnlich verhält es sich bei den positiven Biegemomenten mit einer Reduzierung von M = 503,04 kNm auf M = 375,97 kNm. Durch das Aufreißen des Querschnitts verringert sich die Steifigkeit, so dass die Stützenlasten zu einem größeren Teil direkt in den Boden eingeleitet und nicht erst über den Fundamentbalken zur Seite hin verteilt werden. Die Verformungen werden größer und damit auch die Bettungsspannungen (unteres Bild). Lag die maximale Bodenpressung zuvor noch bei 433 kN/m, ist diese bei nichtlinearer Rechnung des Querschnitts auf 540 kN/m gestiegen.

Berechnung komplett nichtlinear (Querschnitt + Bettung)

Eine Rechnung mit Berücksichtigung eines nichtlinearen Stahlbetonquerschnitts und unter Anwendung einer nichtlinearen Last-Verformungs-Kurve für den Boden ist zwar am aufwändigsten, liefert jedoch auch die genauesten Vorhersagen über die auftretenden Beanspruchungen und Verformungen. Die in der Rechnung benutzte Lastverformungskurve besitzt zu Beginn die gleiche Steifigkeit wie in Rechnung 1 und 2, wird dann jedoch weicher. 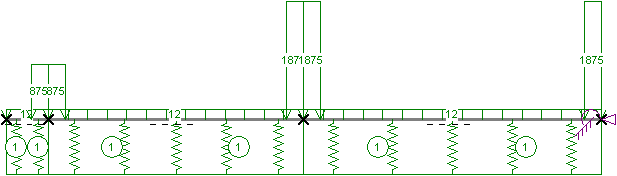Werden Nichtlinearitäten sowohl bei der Bettung als auch beim Querschnitt benutzt, gestaltet sich der Iterationsprozess ungleich schiweriger. Aus diesem Grund war es erforderlich, die 6,00 bzw. 7,00 m Balkenabschnitte in jeweils zwei Balken zu unterteilen. 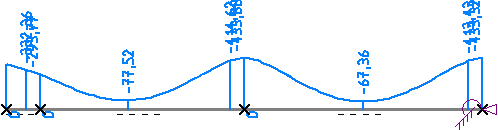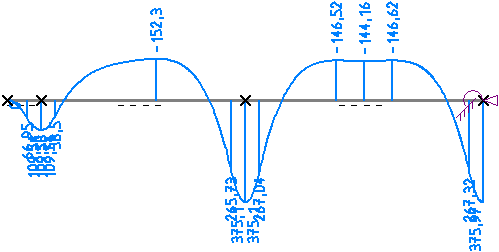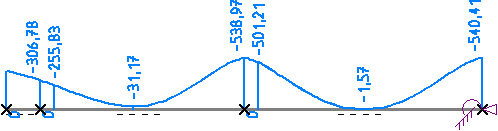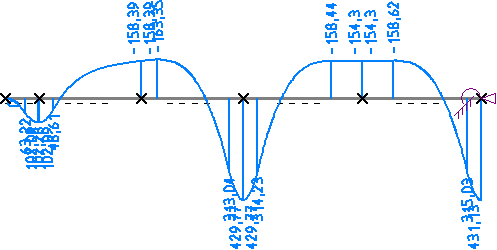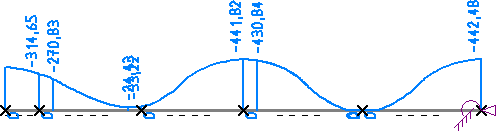In den Ergebnissen sieht man, dass durch den weicher werdenden Boden die Umlagerung wieder in die andere Richtung stattfand. Die Beanspruchungen des Balkens (Biegemoment) sind wieder angestiegen auf M = 431,13 kNm, die Bettungsspannung als Reaktion des Boden ist wieder leicht gefallen auf 442,48 kN/m. Bemerkenswert ist auch, dass im zweiten Balkenabschnitt zwischen 2. und 3. Stütze das Fundament leicht abhebt und die Spannungen in einem Bereich von knapp 0,8 m auf Null gehen (Ausschluss von Zugspannungen).

Hintergründe und Tipps zur Berechnung mit nichtlinearer Bettung

Allgemein setzt eine elastische Bettung beim Übertragungsverfahren immer eine genügend kleine Länge der Stabsegmente beim Übertragungsverfahren voraus. In Abhängigkeit der charakteristischen Länge des gebetteten Balkens wird die anfängliche Segmentlänge zu ca. 10% von L_char angenommen. Eingangswerte zur Berechnung von L_char sind die Biegesteifigkeit des Balkens und die Bettungssteifigkeit.
Da sich jedoch im Laufe der Rechnung sowohl die Biegesteifigkeit infolge Aufreißen als auch die Bettungssteifigkeit ändert, wird sich im Normalfall die charakteristische Länge verkleinern. Die dann im Endeffekt zu groß benutzte Segmentlänge wirkt sich negativ auf den Iterationsprozess auf. Als erstes verringert sich die Genauigkeit der Rechnung, da intern mit einer Näherung für die elastische Bettung gearbeitet wird. Ungenaue Ergebnisse vermindern jedoch auch die Qualität der Gradienten, die beim Übertragungsverfahren benutzt werden. Als letztes kommt noch hinzu, dass durch das Übertragungsverfahren Stabanfangswerte entweder sehr stark gedämpft werden oder sich aufschaukeln können. Beanspruchungen infolge Biegemoment können so sehr schnell oberhalb der maximalen Querschnittstragfähigkeit liegen.

Aus diesen Gründen sollte auf folgende Punkte geachtet werden, wenn die Rechnung nicht konvergiert:

• Verringerung des Wertes für die anfängliche Größe der Stababschnitte oder Erhöhung der minimalen Stabteilung zu Beginn der Rechnung
• statt eines Balkens diesen in evtl. zwei oder drei Balken teilen
• Erhöhung der Anzahl der Lastschritte und Wahl eines Lastverlaufs mit anfänglich sehr kleinen Steigerungen
• Erhöhung der Abbruchgenauigkeit beim Übertragungsverfahren (kleinere Abbruchschranke), damit werden die Werte für die Steifigkeitsmatrix genauer bestimmt
• Vermeiden von starken Gradientenänderungen in der Last-Verformungs-Kurve für den Boden bzw. allgemein für die elastische Bettung. Die Kurve sollte nach Möglichkeit nur so weit modelliert werden, wie es für die Rechnung und das Endergebnis erforderlich ist.